Let's assume you're from the United States and are used to describing your weight in lbs. Let's also assume that you have a friend from France who is used to describing his/her weight in kilograms (kg). How would you describe to your friend how much you weigh?
The problem here is that both of you are using different units: you're using units of lbs and your friend's using units of kg. Like most people in the 21st century, you would google how many lbs are in a kg and would get something like this.
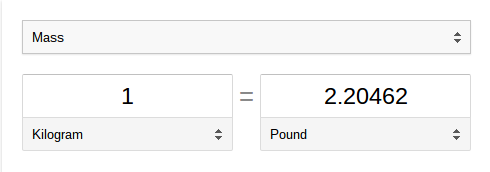
What you have just googled is called a conversion factor, which allows you to convert from one unit to another! Let's talk about what exactly a unit is before continuing.
A unit is a dimension of either mass, length, time, or some combination. Earlier when we were talking about lbs and kgs, we were using units of mass. When you describe to your friend how much more time you'll be, you're using units of time. When you measure your height, you're using units of length. Throughout your scientific career, you'll undoubtedly come into some more complicated units. Consider the unit for energy, the Joule (J):
What that says is that the unit for energy, a Joule, is equivalent to a kg times a second squared all divided by meters squared. Isn't that a crazy unit? Don't worry, we won't deal with anything that complicated yet.
Reviewing fractions and exponents may be of help for understanding a few parts of this post. If you find yourself having trouble with any of the math, check out this post.
Let's return to our earlier example about converting between lbs and kgs. Your poor friend still doesn't know how much you weigh! Before you can tell him, what do these expressions all have in common?
`5/5`, `x/x`, `(afg)/(afg)`
That's correct, they all equal 1. How about this one?
`(kg)/(kg)`
Just like before, this equals 1. When performing dimensional analysis, you can multiply and divide units just as if they were variables. For example:
`J/(atm)((atm)/L)`=` J/L`
The atm unit cancels out, leaving just J on top and L on bottom. That's all that dimensional analysis is! Now we can finally tell your friend how much you weigh. Let's say you weigh 130 lbs.
`130 lbs((1 kg)/(2.2 lb))=59 kg`
By multiplying our original unit by the conversion factor and cancelling out the units, we now get our weight in kg! Note that you have to multiply the conversion factor in a way that the units cancel out. Here's what not to do:
`130 lbs((2.2 lb)/(kg))`=`(286 lb^2)/(kg)`
Now you just end up with an answer that makes no sense! What in the world is a `(lb^2)/(kg)`?! When performing dimensional analysis, write the conversion factor to cancel out the unwanted unit Let's do a couple practice conversions.
#1. Convert `2 atm` to units of `Pa`. The conversion factor is `(101325 Pa)/(atm)`
Since we want units of Pa (Pascal), we want to write the conversion factor as to cancel out atm (atmospheres). This is done as such: `2 atm((101325 Pa)/(atm)) `=`202650 Pa`
#2. Convert `(5 m)/s^2` to units of `(ft)/(hr^2)` The conversion factors are:`(39.4 ft)/m` and `(3600 s)/(hr)`
This one is a bit more tricky as we're dealing with two conversion factors at once, with one of the units squared. Since we want ft (feet) on the top, we want to cancel out the m (meters):
`(5 m)/s^2((3.3 ft)/m)`=`(16.5 ft)/s^2`
Now the meters cancel out and we get `(16.5 ft)/s^2`. Now we want to convert `s^2`(seconds squared) to `hr^2` (hours squared). Since the units are squared, we have to square the conversion factor.
`(16.5 ft)/s^2((3600 s)/(hr))^2= (213840000 ft)/(hr^2)`
That is a big number! Hopefully you are now able to do basic unit conversions. Note that, in the process of doing dimensional analysis, The actual value of whatever's being converted doesn't change. You will still be the same weight after converting and back (sorry, dimensional analysis won't help you lose weight), you're just expressing the unit in a different scale. In the next section we'll look at how to deal with really big numbers, like the one above, or really small numbers.
Units behave slightly differently from variables in the regard of operations. In variables, we can add x + y together with no problems. With units, there are only certain conditions in which we can do so:
Quantities can only be added and subtracted if they are in the same unit.
This means that we cannot add a meter and a centimeter together without first converting the two into the same unit. Likewise, we cannot add a Joule and a Tesla together, seeing as they're both completely different units.
The rules for multiplication and division are more lax:
Quantities may be multiplied and divided regardless of their unit.
A `L` multiplied by an `"atm"` simply becomes a new unit known as the `L*"atm"`. As you encounter more units, you'll discover that most units are just various combinations of different other units multiplied or divided by each other.
Something important to take note of is dividing a unit by itself. This creates a unitless number, which, as the name implies, is a number withouta unit. For example, if you were to were to calculate `(4 L)/(2 L)`, you would end up with the number 2 since the units of `L` cancel out.
While science often times requires a lot of time and work, scientists themselves can be quite lazy. Instead of writing out huge numbers such as 213840000, we express the numbers in scientific notation.
`213840000= 2.14*10^8`
This saves a lot of time and space! Here's how to convert to scientific notation:
1. Find the decimal point. If there is no decimal point, Place one where at the far right end of the number.
2. Move the decimal point one number at a time until there is only one number to the left of it. Count how many times you moved the decimal. This will be your exponent.
3. If the decimal point started on the left, write the exponent as a negative. If the decimal point started on the right, write the exponent as a positive. The exponent will always be raising base 10.
Here are some practice problems:
#1. Convert 424000 to scientific notation.
1. Since there is no decimal point, write one at the right of the number: (424000.).
2. Now move the decimal point to the left until there is only one number to the left of it: 4.24000. Count how many times you moved the decimal (5 times)
3. Raise base 10 to this exponent. Since you started on the right, this exponent will be positive.
The final answer will be `4.24*10^5`
#2. Convert 0.00006924 to scientific notation
1. The decimal point is at the left of the number. Move it one digit at a time until there is only one number to its left. Count how many times you did this (5 times).
2. Since the decimal started on the left, the exponent will be negative. Raise base 10 to this exponent.
The final answer will be `6.924*10^5`
Let's say I was doing an experiment and had 1000000 g (grams) of a particular molecule. Instead of writing that number over and over in my calculations, I can convert it to a smaller version of the unit.. For example, I can convert it to a mg (milligram), or ng (nanogram) in order to save myself some effort. The prefixes deci-, centi-...,nano-...etc allow us to do exactly that. These are called metric prefixes. Here's the scale:
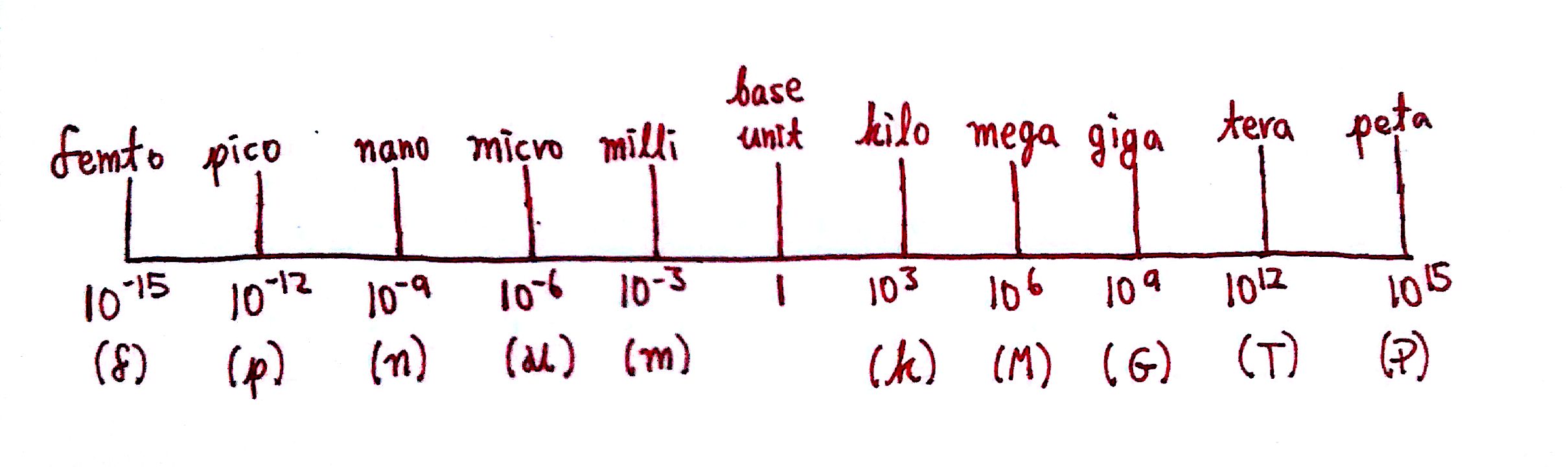
The little letters under the scale are the shorthand way of writing the prefixes e.g a kilometer is written as km. Using this, we can deal represent units as larger or smaller versions of that unit. Let's do an example:
#1. Convert 60000L to ML.
As we see on the scale, M (mega) is the prefix for `10^6`. Therefore, 1 ML (mega-liter) is equal to `10^6L`. The conversion factor is `(1 ML)/((10^6 L)`.
`60000 L((1 ML)/(10^6 L))=0.06 ML`
This is certainly a much more manageable number than 60000L was! Metric prefixes simply save us the time of writing out large numbers.

Due to the number of units, there exists a standard for units to be used in science. In science, we don't use the unit hr (hours), but rather s (seconds) because s has been chosen as the SI unit. The reason this exists is to avoid situations like the one depicted in the above comic. There are 7 fundamental SI units:
time: s (seconds)
length: m (meters
mass: kg (kilogram)
electric current: I (ampere)
temperature: K (Kelvin)
amount: mol (mole)
luminous intensity: cd (candela)
As you continue on through science, you'll undoubtedly come across many different kinds of units. Always remember to convert back to SI units whenever possible, unless stated otherwise! i.e don't write your final answer in `g/(mm)`, write it in `(kg)/m`. In most cases, you'll be using SI units.
Dimensional analysis allows us to convert units between different scales.
Converting units does not change the actual value of the unit. If you convert it back to the original unit, the number should be the same
Scientific notation lets us write really large or really small numbers in a more efficient way.