The half life, often abbreviated as`(t_(1/2))` , is the duration of time for a material to decay 50%.
Let's mathematically look at the idea of a half-life. Specifically, this example applies only to first order reactions. Imagine you have 100g of a material with a half life of 1 minute. Here's a table showing the amount of material over a period of time.
Time `("min")` |
`0` |
`1` |
`2` |
`3` |
`4` |
`5` |
Amount `(g)` |
`100g` |
`50g` |
`25g` |
`12.5g` |
`6.25g` |
`3.125g` |
As we can see in the table, every minute that goes by corresponds to 1 half life and thus the amount decreases to 50% what it was before. At 1 minute, we have 50% of the original amount. At 2 minutes (2 half-lives), we have 25%. 3 minutes (3 half-lives), 12.5%, ad nauseum. The amount that decays away is not the same for each half life, only the percentage that decays is.
If we were to graph this with amount in grams on the y-axis and time in minutes on the x-axis, we'd get a graph that looks like:
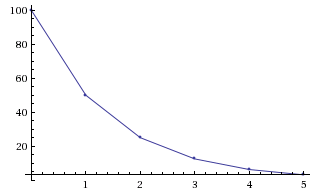
All of this is to say that for a first order reaction, the half life does not depend on the amount of material.
For first-order decay:
`t_(1/2)=0.693/k`
Notice that the half life only depends on `k` for a first-order decay. The example above applies to first-order decays, as the half life is independent of concentration. For first-order decay, it doesn't matter whether the starting amount is 100g or 100 million tons - the half life will still be the same.
Additionally, here's a convenient formula we can use to calculate the amount of material left:
`A=A_0*(1/2)^(t/h)`
`A= "final amount"`
`A_0= "initial amount"`
`t= "time"`
`h= "half-life"`
#1. The half life of the C-14 isotope if 5700 years. You find a piece of wood with 40% of the C-14 contained in other living materials. How old is the piece of wood? Assume first-order decay.
We can use the formula `A=A_0*(1/2)^(t/h)` to solve for `t` . Rearranging the formula, we get:
`t=(-h*("log"(A/(A_0))))/("log"(2))`
`t=(-5730*("log"(0.4)))/("log"(2))`
Answer = 7600 years old
For second-order decay:
`t_(1/2)=1/(k[A]_0)`
For second-order decay, the half life depends both on `k` and the initial concentration. This means that the half life is not constant for a process but changes depending on concentration i.e the first half life will be different from the second, which will be different from the third, etc. In fact, for second-order decay, each half life is double the previous one. If the first half life was 5 minutes, the second will be 10, the third 20, etc.
For zeroeth-order decay:
`t_(1/2)=[A]_0/(2k)`
Just like with second-order decays, the half life of a zeroeth-order decay depends on both `k` and the initial concentration. The difference is that as the initial concentration increases, the half life increases as opposed to with second-order decays, where the half life decreases as concentration increases.
1. The half life is the time it takes for a material to decay to 50% of its original amount.
2. For first-order decay, the half life is constant and does not depend on the concentration.
3. For second-order decay, the half life is dependent on both `k` and the initial concentration. The half life increases as the concentration decreases.
4. For zeroeth-order decay, the half life is dependent on both `k` and the initial concentration. The half life will decrease as the initial concentration decreases.
#1. C-14 Dating
C-14 dating utilizes the decay of the carbon-14 isotope in order to determine the age of organic material. The decay reaction involves carbon-14 decaying into a stable nitrogen-14 molecule:
`C_6^(14) rArr N_7^(14) + e^-`
The amount of the C-14 isotope is approximately 1% of all carbon contained in living things and is constantly being replentished. In other words, the amount of C-14 in the atmosphere has essentially remained constant. Once a being passes, they stop intaking C-14 and thus the amount of C-14 in the body at death remains the amount that will, overtime, decay. By comparing the amount of C-14 in the environment to the amount of C-14 in the corpse, we can accurately determine the age of the specimen. The half life of the C-14 isotope is roughly 5730 years, for reference.
#2. Uranium-238
Just like with C-14, we use the amount of U-238 isotope in rocks to determine the age of the rock. The half-life of U-238 is approximately 4500 million years and eventually decays to Pb-206. By comparing the amount of U-238 to the amount of Pb-206, we can accurately determine the age of the rock.