So far, we've gone over the ideas of chemical equilibria and the equilibrium constant. In this section, we're going to go over a technique that allows us to predict the position of equilibrium.
The technique we're going to use is the construction of an ICE table, where "I" stands for "Initial," "C" for "Change," and "E" for "Equilibrium."
We're going to go step by step into the construction of a basic ICE Table.
Consider the reaction below:
`2NH_3 ↔ N_2 + 3H_2`
You're given a mixture containing `0.5 "moles" NH_3 , 0.5 "moles" N_2 , "and" 0.3 "moles" H_2` in a `2 "L"` container. Determine the equilibrium concentrations. `K_C= 0.54`.
We're given an initial starting position and want to find the final equilibrium position. To do this, we're going to construct an ICE table.
ICE tables will always have 3 rows (for I,C, & E). Since we have 3 species, we're going to have 4 columns (one of the columns just contains the I, C, and E). The starting table should look something like this:
`2NH_3` |
`N_2` |
`3H_2` |
|
I |
|||
C |
|||
E |
Initial (`"I"`)
Now, we're going to put in the initial conditions. For ICE tables, we use either concentration or pressure. First, convert all of the values to units of concentration. As a brief reminder, the units of concentration are `"moles"/"L"` . Put those values into the `"I"` row of the table, representing the initial position.
The procedure for using pressure in ICE tables is nearly identical to that of concentration. The only difference is, well, we're using pressure.
`2NH_3` |
`N_2` |
`3H_2` |
|
I |
`0.25 M` |
`0.25 M` |
`0.15 M` |
C |
|||
E |
Change (`"C"`)
Now, we're going to fill in the `"C"` row. The `"C"` row stands for the change in the reaction's position. Since we don't know the change, we're going to represent the change as a variable `x` .
Recall from stoichiometry and your understanding of chemical equations that the coefficient in front of a reactant indicates the stoichiometric amount of the reactant that reacts. For this reaction in particular, every `"mol"` of `N_2` that reacts must react with `3 "mol" H_2` to form `2 "mol"` of `NH_3` . Therefore, the `x` value will be different for each species because a different amount of each species is reacting:
`2NH_3` |
`N_2` |
`3H_2` |
|
I |
`0.25 M` |
`0.25 M` |
`0.15 M` |
C |
`-2x` |
`+x` |
`+3x` |
E |
The change term is probably the most confusing part of ICE tables. Think of it this way: we're assuming that the reaction will proceed in the rightward direction since the `K_C` is a somewhat large value. This means that the `NH_3` is going to break apart to form `N_2` and `H_2` . Since the amount of `NH_3` that dissociates is going to be `2x` the amount of `H_2` that is produced, we can express the change in `NH_3` as `-2x` and the change in `N_2` as `+x` . The same logic applies to `H_2` : since the amount of `H_2` that's produced is the `3x` the amount of `N_2`, we can express the change in `H_2` as `+3x` .
Another way to think of it: equations express the change in a reactant in the coefficient. The x term is always going to be multiplied by the coefficient of the species. If the amount of the species is decreasing, the change term is negative. If the amount of the species is increasing, the change term is position.
Equilibrium (`"E"`)
The `"E"` is going to be the position at equilibrium. Notice that the equilibrium position is just the initial position plus whatever the change was. This means we just add the `I` and `C` boxes:
`2NH_3` |
`N_2` |
`3H_2` |
|
I |
`0.25 M` |
`0.25 M` |
`0.15 M` |
C |
`-2x` |
`+x` |
`+3x` |
E |
`0.25 - 2x` |
`0.25 + x` |
`0.15 + 3x` |
That's all there is to the construction of an ICE table!
The Law of Mass Action for this reaction would normally be written as:
`K_C=([N_2][H_2]^3)/[NH_3]^2`
where the concentrations are the concentrations at equilibrium. Since we don't know the actual values of equilibrium, we can express them in terms of `x` , which is exactly what we did in the `"E"` component of the ICE table. We can therefore write the Law of Mass Action expression using the ICE table:
`K_C=([0.25+x][0.15+3x]^3)/[0.25-2x]^2`
Since we're given `K_C=0.54` , we can plug in `0.54` for `K_C` .
`0.54=([0.25+x][0.15+3x]^3)/[0.25-2x]^2`
Later on in this post, we'll go over a technique that allows us to simplify these polynomials. For now, I plugged the equation into WolframAlpha and got `x=0.057` . If we plug in this value into all of `"E"` expressions, we get:
`[NH_3]=0.25-2(0.057)=0.136`
`[N_2]=0.25+(0.057)=0.307`
`[3H_2]=0.15+3(0.057)=0.321`
We've just solved for the equilibrium concentrations! We can check if the concentrations work out by solving for the `K_C` corresponding to these concentrations:
`K_C=([0.307][0.321]^3)/[0.136]^2=0.55`
With consideration for rounding errors, this is the same as our given `K_C` of `0.54` !
The construction of ICE Tables can be broken down into several steps:
1. Draw the ICE table with sufficient boxes for all of your reactants.
2. In the `I` section, write down the initial concentrations of each of the reactants.
3. In the `"C"` section, write down the change of each species in terms of an variable `x` . The `x` value will be multiplied by the coefficient of the reactant. The sign of the change will be based off which way the reaction is going: if `K_C` is large, the reaction will proceed to the right and the opposite for if `K_C` is small.
4. The `"E` boxes will be the equilibrium concentrations and are found by adding the `"I"` and `"C"` boxes.
In order to solve for the `x` term, the `K_C` value must be given. Solve for `x` using the Law of Mass Action expression and use the value of `x` to solve for the `"E"` concentrations.
There are two techniques we're going to go over to make solving for `x` as systematic as possible. The first is a familiar one in the quadratic formula, and the second is called the small number approximation.
Quadratic Formula
From algebra, we know that for any equation in the form of `ax^2 + bx + c=0` , `x` can be solved as:
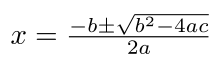
This can be used in equilibrium expressions. With ICE tables, we'll commonly get expressions like the following:
`K_C=x^2/(1-x)`
Let's say that, for this equation, `K_C=0.3` . We can solve for x by using the quadratic method:
`0.3=x^2/(1-x)`
`0.3(1-x)=x^2`
`0.3-0.3x=x^2`
`x^2+0.3x-0.3=0`
Since we now have the equation in quadratic form, we can use the quadratic formula! `a=1 , b= 0.3, "and" c=-0.3` . We should get values of `x=0.42` and `x=-0.71` . Since we know `x` can't be negative, `x=0.42` must be the correct answer.
Here's a problem to illustrate when the quadratic formula is used.
#1. You start off with only `0.7M A` in the following reaction:
`A ↔ B + C`
Calculate the equilibrium concentrations if `K_C` for the reaction is `0.2` .
The first step is to construct an ICE table:
`A` |
`B` |
`C` |
|
I |
`0.7 M` |
`0 M` |
`0 M` |
C |
`-x` |
`+x` |
`+x` |
E |
`0.7-x` |
`+x` |
`+x` |
The equilibrium expression is therefore:
`K_C=((x)(x))/(0.7-x)=x^2/(0.7-x)`
Since we're given the `K_C` value, all we have to do is solve for `x` .
`0.2=x^2/(0.7-x)`
`0.2(0.7-x)=x^2`
`0.14-0.2x=x^2`
`x^2+0.2x-0.14=0`
Using the quadratic formula, we get `x=-0.49` and `x=0.29` . Since `x` must be positive, we know `x=0.29` .
Now all we have to do is plug `x` back into the `"E"` concentrations.
`[A]=0.7-0.29=0.41`
`[B]=0+0.29=0.29`
`[A]=0+0.29=0.29`
We can check if this corresponds to the correct `K_C` :
`K_C=(0.29)^2/(0.41)=0.21`
Accounting for rounding errors, this is correct!
Answer: `[A]=0.41, [B]=0.29,[C]=0.29`
Small Number Approximation
Often times, you'll get expressions that are too complicated to solve by hand. The technique we're going over in this section is called the small number approximation or successive approximations. In order to use the small number approximation, `K_C` must be small. The metric I was taught was 2 orders of magnitude less than the concentration, but in general, one can apply the small number approximation to any `K_C<10^-4` . For example:
`3x10^(-8)=x^3/(2-x)`
We certainly can find some way to solve this by hand, though it would be time consuming and impractical. Instead, we can approximate `x` as negligibly small.
Since `K_C` is very small, we know that the change, `x` , is going to be very small. This means that `(2-x)≈2` , since `x` is so small it can be neglected.
`3x10^(-8)=x^3/(2-x)≈ x^3/2`
Notice that the small number approximation only applies for adding and substracting. When `x` is raised to a power, we cannot use the small number approximation.
Small number approximations, when valid, save a significant amount of time. Consider the following equilibrium expression:
`4x10^(-10)=(7-3x)^2/(x^4)`
Since `K_C` is small, we can apply the small number approximation:
`4x10^(-10)=(7)^2/(x^4)`
`x^4=(7^2)(4x10^(-10))`
`x^4=1.96x10^(-8)`
`x=0.012`
While we can't use the small number approximation in all cases, there will be many cases that we can. As such, it's important to become familiar with it. To summarize:
1. The small number approximation can only be applied when `K_C` is small.
2. The approximation only applies for addition and subtraction.
ICE tables are best learned through practice. There will be a couple problems in the end of section review questions that utilize ICE tables should you find yourself needing problems.