An oxidation-reduction reaction, often simplified to redox (from reduction-oxidation), is a reaction that involves the transfer of electrons. When a molecule is oxidized, it loses electrons. Likewise, when a molecule is reduced, it gains electrons. An easy way to remember this is the mneumonic
OIL RIG
which stands for Oxidation is loss, Reduction is gain.
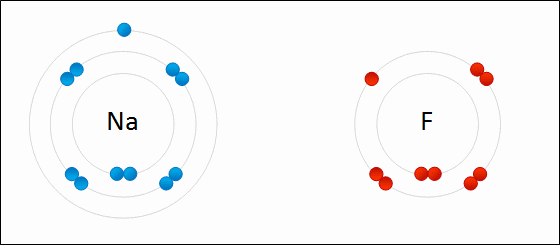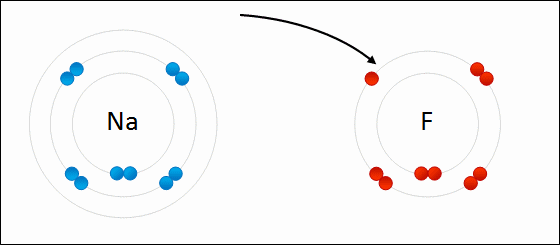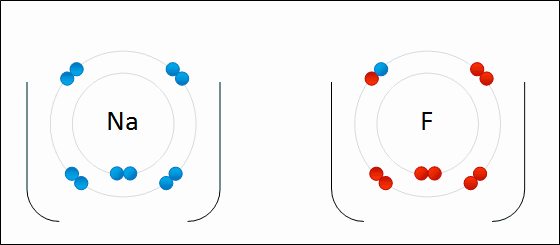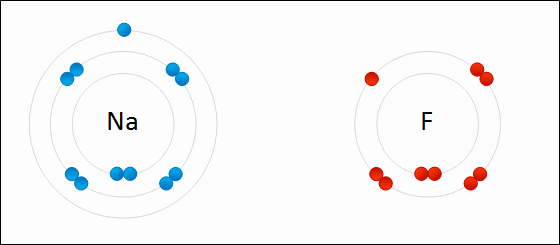
In this example, sodium loses one electron whereas fluorine gains one electron. We can therefore say that sodium has been oxidized and fluorine has been reduced.
When an oxidation reaction occurs, an equivalent reduction reaction must occur alongside it. The two happen simultaneously and can never be done individually. We say that the species being reduced is the oxidizing agent and conversely the species being oxidized is the reducing agent. This can be confusing, but makes intuitive sense:
Imagine you have two molecules, A and B. Molecule B takes an electron from molecule A. Because of this, B is now reduced and A is oxidized. In the course of taking an electron from A, B itself became reduced. Therefore we say that A is the reducing agent, since it caused B to become reduced. Likewise, A is the oxidizing agent seeing as it caused B to become oxidized. We can summarize this by the following two statements:
If a species is oxidized, it is the reducing agent.
If a species is reduced, it is the oxidizing agent.
Oxidation States
Oxidation states allow us to quantify oxidation-reduction reactions. Take this following reaction for example:
`Fe_2O_3 + 3CO rArr 2Fe + 3CO_2`
We can use oxidation states to determine which species are being oxidized and which are reduced. The change in oxidation state is what indicates whether a species is oxidized or reduced. When the oxidation state increases, the species is oxidized. When the oxidation state decreases, the species is reduced. There are a couple rules for determining oxidation state:
1. The oxidation state of an element by itself (`O_2, Fe, F_2, S_8`) is always 0.
2. The oxidation state of a monatomic ion is the charge on the ion e.g `F^-` has a oxidation state of -1.
3. The sum of all oxidation states in a neutral molecule is equal to 0.
4. The sum of all oxidation states in a polyatomic ion is equal to the charge on the ion e.g the sum of the individual oxidation states of C and O must be equal to -2 for `CO_3^(2-)`.
Additionally, here are some of the common oxidation states:
| Species |
Oxidation State |
Followed |
Exceptions |
| Alkali Metals |
+1 |
Always |
None |
| Alkaline Earth Metals |
+2 |
Always |
None |
| Oxygen |
-2 |
Almost always |
Peroxides: `H_2O_2` |
| Hydrogen |
+1 |
Almost always |
Metal Halides: `LiAlH_4` |
| Fluorine |
-1 |
Always |
None |
| Halogens |
-1 |
Almost always |
In combination with O or F |
Now we can completely describe redox reactions:

#1. Determine the oxidation state for each of the atoms in `BaO_2`.
We know that the sum of the oxidation states must equal 0 since the overall charge on the molecule is 0. From the table above, we know that the oxidation state of `O` is -2. Since there are two of them, there is a total negative charge of 2(-2) = -4
`Ba` must have a charge of +4 in order to balance out the -4 from the two oxygen atoms. The answer is therefore +4 for `Ba`, and -2 for each `O` atom.
Answer: `Q_(Ba)= +4, Q_O= -2`
#2. Determine the oxidation state for each of the atoms in `CrO_4^(2-)`.
We know that the sum of all the oxidation states must be -2 because the net charge on the molecule is -2.
Additionally, we know that each `O` atom has an oxidation state of -2. Since there are 4 of them, the total oxidation state for the oxygens must be 4(-2) = -8.
The `Cr` atom has to have an oxidation state such as to leave the total oxidation state as -2. If you want a systematic way of solving this, you can set up an equation:
`Q_(Cr) + 4Q_O = -2`
`Q_(Cr) + (-8) = -2`
`Q_(Cr) = +6`
Where `Q_(Cr)` and `Q_O` are the oxidation states of `Cr` and `O` respectively.
Answer: `Q_(Cr)= +6, Q_O= -2`
#3. Determine the oxidation states of each atom in HBrO
There is no charge on this molecule, so the sum of the oxidation states must be 0.
We can see from the chart above that `O` and `H` always have oxidation states of -2 and +1 respectively. Since the states must add up to 0, we can setup another equation:
`Q_H + Q_(Br) + Q_O = 0`
`Q_(Br) = - Q_H - Q_O`
`Q_(Br) = -(+1) - (-2) = +1`
Answer: `Q_H= +1, Q_(Br) = +1, Q_O=-2`
#4. Determine the oxidation states for each atom in `(NH_4)_2MoO_4`
Recall from the section on polyatomic ions that `NH_4^+` has a net charge of +1. Each `O` atom has a charge of -2. The equation is therefore:
`2Q_(NH_4) + Q_(Mo) + 4Q_O = 0`
`Q_(Mo) = -2Q_(NH_4) - 4Q_O`
`Q_(Mo) = -(+1) - 4(-2)=+7`
Answer: `Q_(Mo) = +7, Q_(NH_4)=+1, Q_O=-2`
Balancing Redox Reactions
Balancing oxidation-reduction reactions is slightly more complicated than balancing equations, but nothing unmanageable. For a reminder on how to balance chemical equations:
Chemical Equations
In oxidation-reduction reactions, the atoms may be balanced, but the electrons may not be. For a redox reaction to be balanced, both atoms and electrons must be balanced. For example:
`Cu + Ag^+ rArr Cu^(2+) + Ag`
Let's first look at whether the atoms are balanced or not. There is 1 `Cu` and 1 `Ag` on both sides of the equation, so the atoms are balanced. Now let's consider the charge: on the reactants side, there is a net charge of +1 on the `Ag` whereas on the products side there's a net charge of +2 on `Cu`. This indicates an imbalance of electrons that we have to account for. To do this, we use half-reactions.
`Cu rArr Cu^(2+) + 2e^-`
`Ag^+ +e^- rArr Ag`
We can separate the reaction to include an oxidation half-reaction and a reduction half-reaction. Just like the name implies, the oxidation half-reaction only contains the half of the reaction that is being oxidized. Conversely, the reduction half contains only the species being reduced.
You've probably noticed that there are electrons written with the reaction. This is so that we can account for the number of electrons. In half reactions, these electrons are treated just like reactants. Because of this, they have to be balanced.
`Cu rArr Cu^(2+) + 2e^-`
`2Ag^+ +2e^- rArr 2Ag`
By multiplying the bottom half reaction by 2, we now have 2 electrons on both sides. Now we can add the two half-reactions back together.
`Cu + 2Ag^+ + 2e^- rArr Cu^(2+) + 2Ag + 2e^-`
By cancelling out the electrons, we now have a balanced oxidation-reduction reaction.
`Cu + 2Ag^+ rArr Cu^(2+) + 2Ag`
#5. Balance the following redox reaction: `NaCl + Br_2 rArr NaBr + Cl_2`
Right off the bat we can see that the reaction is unbalanced. Since we know that the reaction is a redox reaction, we can hold off on balancing the reactants and first write out the half reactions. First, identify which species are being oxidized and which are being reduced.
`Cl` is going from -1 to 0 while Br is going from 0 to -1. Thus, `Cl` is being oxidized while `Br` is being reduced.
`Cl^- rArr Cl_2 + e^-`
`Br_2 + e^- rArr Br^-`
The half reactions themselves are unbalanced. Let's fix that.
`2Cl^- rArr Cl_2 + e^-`
`Br_2 + e^- rArr 2Br^-`
Now that the half reactions and the electrons are balanced, we can recombine the half-reactions.
Answer: `2Cl^- + Br_2 rArr Cl_2 + 2Br^-`
Summary
1. An oxidation-reduction reaction, often compacted to redox, involves a transfer of electrons.
2. Redox reactions cannot occur without both components i.e one can never have just a reduction reaction without the oxidation component. The two happen simultaneously.
3. In order to balance redox reactions, one has to balance both the atoms and the electrons.